• Title: The effect of the environment on the Faber Jackson relation
• Authors: Paola Focardi, Nicola Malavasi
• First Author’s Institution: Universit´a di Bologna, Italy
Introduction
If you plot the rotational speed of a collection of spiral galaxies versus their luminosities, you’ll find a tight relationship between the two: the brighter spirals rotate faster. This is known as the Tully-Fisher relation, and it was discovered in 1977. It’s a simple rule and it’s found to be nearly universally true.
Such a relation can be extremely useful in astronomy. For example, since we know that there is a tight relationship between a spiral galaxy’s rotational speed and its total brightness, if we can measure its rotational speed then we can also infer its brightness. Then, if it appears dimmer than expected, we can infer that this is due to its distance and we can calculate how far away it must be. (Of course, this is a simplified picture— other things such as dust can dim a galaxy.)
The Tully-Fisher relation is a useful tool for measuring the brightnesses of spiral galaxies, but is there a similar tool we can use to characterize other types of galaxies? Ellipticals don’t have a single rotational plane, so their rotational velocity isn’t well-defined. Instead, we can define a new property, the velocity dispersion, usually written as σ (sigma). Roughly speaking, it’s a measure of the uniformity of the velocities of the stars in the galaxy. If they all move about with the same velocity, the galaxy has a very low velocity dispersion. Elliptical galaxies with larger velocity dispersions are brighter, in what’s known as the Faber-Jackson relation.
Improving Faber-Jackson
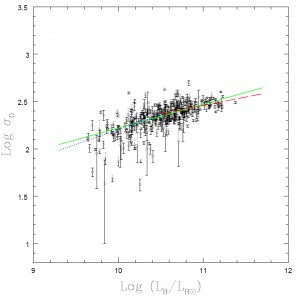
The Faber-Jackson relation for the galaxies studied in the paper. Notice that while the relationship is clear, there is still scatter about the trend line. (Figure 3 in the text)
None of these relations are exact. Instead, there is some scatter in the relationships, as you would expect. An ongoing question is how we might reduce the scatter in these relationships: for example, we can introduce a third parameter, say galactic size, and see if the galaxy’s total brightness is better determined by some combination of its size and velocity dispersion. The mathematical relation between the size, velocity dispersion, and brightness of an elliptical galaxy is called the “fundamental plane.”
The authors of this paper are concerned with just the original Faber-Jackson relation, but they want to know if the scatter in the relation might be related to something different. Specifically, they’re interested in the role of environment. A galaxy’s environment usually refers to whether it belongs to a cluster, or if it’s in the field. Cluster environments are denser, contain lots of hot gas, and galaxies in them are more likely to collide and interact with one another.
The authors characterize a galaxy’s environment by finding how many neighbors it has within one and a half megaparsecs. They then divide their galaxies into low- and high-density samples; the galaxies in high-density environments typically have roughly 40 neighbors within a megaparsec and a half, whereas the low-density galaxies might have as few as one or none. Then, it’s just a matter of plotting the Faber-Jackson relation for these two samples and comparing the result.
Conclusions
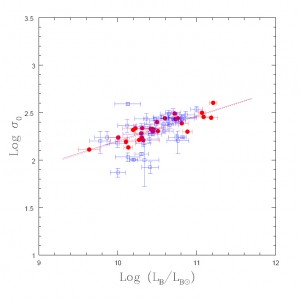
The Faber-Jackson plot, now for the high-density galaxies (red dots) and low-density galaxies (blue). Notice that the red galaxies exhibit much less scatter. (Figure 7 in the text)
The plot on the left shows the result: the high-density galaxies are the red circles, whereas the low-density galaxies are blue squares. Clearly, the galaxies in dense environments have much less scatter in their luminosity-σ relation! Since scatter in the Faber-Jackson relation can be reduced by also considering galactic size, perhaps this effect is the result of a size-environment correlation.
In any case, such results in these empirical relationships are always interesting and useful; they show us that some physical process is at work, determining galaxies’ appearances. Sometimes we have a theoretical mechanism to explain them, and sometimes we don’t. Investigating the origin and nature of these relationships aids us in our attempt to understand galaxy formation and evolution.