Title: New Limits on Early Dark Energy From the South Pole Telescope
Authors: Christian L. Reichardt, Roland de Putter, Oliver Zahn, Zhen Hou
First Author’s Institution: University of California, Berkeley
The expansion of the universe is accelerating. The discovery of this fact was revolutionary in astronomy, and, it turns out, is the type of discovery that will win you the Nobel Prize in Physics. Prior to this result, most people believed the expansion of the universe must be slowing down, since gravity tries to pull matter back together. An accelerating universe means that there must be something pushing on space itself, causing it to expand faster and faster. The exact mechanism for this process remains unknown, and we parameterize our ignorance with the term dark energy.
The current favored cosmological model, known as the model, tells us that roughly 73% of the universe today is composed of this mysterious dark energy (check out this astrobite for a more detailed discussion of this cosmological model). The simplest form of dark energy is known as the cosmological constant and involves an energy whose density is constant in time. In this case, as one looks back in time, the relative importance of dark energy quickly becomes much smaller than that of matter and radiation; this arises from the fact that the density of matter scales as
and the density of radiation scales as
, where
is known as the scale factor and parameterizes the size of the universe
. Thus, at early times in the universe’s history when the universe was much smaller
, its density was dominated first by radiation and then by matter. Dark energy’s influence only becomes apparent at much later times, such as the present.
However, there are alternatives to the cosmological constant model in which the influence of dark energy in the early universe was not negligible in comparison to that of radiation and matter. These types of theories are known as early dark energy (EDE) models because they predict a strong dark energy effect at early times. The authors of this paper consider such a model, and constrain the density of EDE using the latest measurements of the temperature fluctuations of the cosmic microwave background (CMB) from the South Pole Telescope (SPT).
How can high-resolution measurements of the CMB constrain the existence of dark energy in the early universe? The amplitude of the CMB’s temperature fluctuations as a function of angular scale is sensitive to several important parameters, including the densities of matter, radiation, and dark energy (just recently, measurements of the CMB provided evidence for the existence of dark energy independent of any other measure of the universe’s expansion rate). The existence of EDE would imprint a strong signature on the CMB, and we can search for this signature in the CMB power spectrum. The power spectrum characterizes the size of temperature fluctuations as a function of multipole , where large (small)
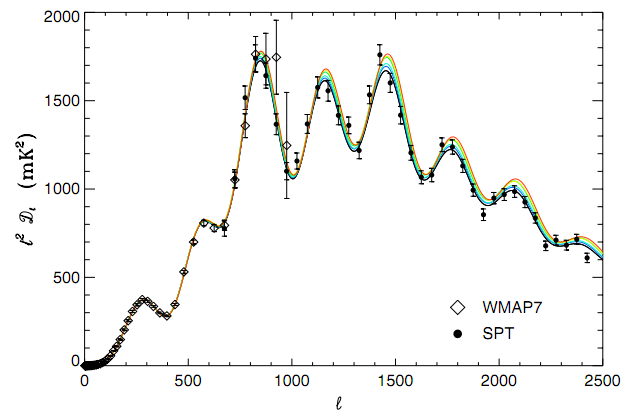
corresponds to small (large) scales on the sky. The multipole number is similar to the frequency of a wave, in that a larger multipole number corresponds to fluctuations of a smaller physical scale. For a great introduction to the CMB power spectrum, check out this tutorial by Wayne Hu. The CMB’s power spectrum as measured by SPT is shown in the figure below.
The addition of EDE increases the expansion rate in the early universe, which suppresses the growth of matter perturbations. This suppression in turn drives an increase in the amplitude of the temperature anisotropies, most strongly on small scales. Thus, the addition of EDE enhances the peaks in the CMB power spectrum at high . Until recently, the CMB power spectrum had been measured with small errors only at low
by the WMAP satellite (shown on the plot by the open diamonds), but as the effects of EDE are strongest at high
, the WMAP measurements are not sufficient for strong constraints on its existence. However, SPT has a higher spatial resolution than WMAP and is able to measure the small-scale CMB temperature anisotropies with much greater precision. The figure above shows the WMAP and SPT measurements of the CMB power spectrum as well as six different best-fit models with varying EDE density, denoted by
, from 0% (black) to 5% (red). Each of the EDE models is consistent with the WMAP data at large scales, but they differ significantly from each other and from the data at the smaller scales to which SPT is sensitive.
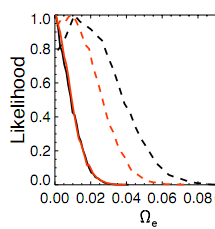
Using the combination of WMAP and SPT measurements, the authors place a strong upper limit on the density of early dark energy. With a confidence level of 95%, the authors find an upper limit . If dark energy existed in the early universe, it did not account for more than 1.8% of the total density of the universe. This is roughly a factor of 3 improvement over the upper limit derived solely from the WMAP data,
. The probability distribution for
derived from the data is shown in the figure to the left. The authors also point out that in the next year, order of magnitude improvements in the measurements of the small-scale CMB power spectrum are expected from surveys like SPT, the Atacama Cosmology Telescope, and the Planck satellite. These improvements promise to further our understanding of the nature of dark energy and its importance in the early universe.



very nice
Good article
Grappig hoor!