Title: Mind the Gap: Tightening the Mass-Richness Relation with Magnitude Gaps
Authors: Andrew P. Hearin, Andrew R. Zentner, Jeffrey A. Newman, Andreas A. Berlind
First Author Institution: University of Pittsburgh
It’s tough to measure the mass of something like a group of galaxies because there is no easy way to do so without making grand assumptions or time intensive observations. At optical wavelengths, you can either use dynamics or weak lensing which require spectroscopic measurements or photometric redshifts, and a complete sampling. Another method is to admit that the physics are tough and try to skirt them by finding scaling relations between the mass and some observable physical characteristic. This actually works quite well, and scaling relations are a common tool in many astrophysical studies. Two of the most common, the Tully-Fisher relation and Fundamental Plane use 2-3 correlated parameters in galaxies to glean new information.
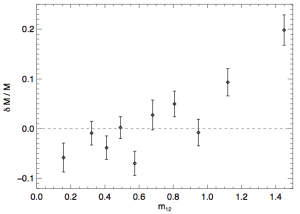
Figure 1: The difference in magnitude between the first and second brightest galaxies in the group (x-axis) vs. the fractional difference in the true mass and the mass-richness relation. The larger the magnitude gap, the more massive a group is at fixed richness.
In this case, the authors look at the relation between the galaxy group mass and richness. Richness is defined as the number of member galaxies in a galaxy group which can be as high as hundreds for some clusters or as low as a few. As you might imagine, massive groups tend to have more members, so the relation has a positive correlation. Therefore, to estimate the mass of a galaxy group, all you need to do is count the members! But wait! Galaxy clusters and groups can be very unique, and two systems with 15 member galaxies may have very different masses. This means there will be scatter in the relationship. The authors investigate reducing the scatter in the relations by invoking a third bit of information; the difference in magnitude between the first and second brightest galaxy in the group. This is called the magnitude gap.
To test whether the magnitude gap carries information about a group’s mass, the authors use a large N-body simulation with galaxies painted onto dark matter sub-halos as a test to identify any trend. In Figure 1 they show that in the simulation, the groups that have large magnitude gaps tend to also be of larger mass than those with smaller magnitude gaps at the same richness. This means the magnitude gap can be used to improve the calibration of the mass-richness relation. In fact, they find that the scatter drops from 33% to 27% taking the magnitude gap into account. This suggests some sort of dynamical connection between the magnitude gap and richness; however, even in the absence of such a connection, we still expect large gap systems to have fewer members simply due to random draws from the luminosity function of galaxies (the Schecter function). Less draws = greater gap. But this should not be the case here because if the magnitude gap were purely statistical, it could not contain any information about the mass that would not already be provided by richness.
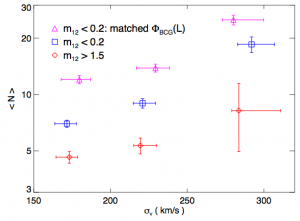
Figure 2: the bias corrected low magnitude gap systems (purple) are much richer for a given velocity dispersion than the systems with a large magnitude gap (red).
Now that the authors have shown that the magnitude gap carries information about the group in the simulations, they do a further test on the Sloan Digital Sky Survey DR7. In the real universe we no longer know the group’s true mass, so the authors choose the galaxy group’s velocity dispersion as a mass proxy. After correcting the sample to avoid biases, the authors show (Figure 2) that at a fixed richness (N) the groups with a large magnitude gap (red) have higher velocity dispersions therefore more mass than those with small magnitude gaps (purple). The authors don’t provide an explanation for this connection between magnitude gap and group mass, but the results agree with a recent paper I summarized on the nature of systems with large magnitude gaps.