Title: Star Formation in Atomic Gas
Author: Mark Krumholz
First Author’s Institution: University of California – Santa Cruz
It is a well-known paradigm that stars form from the gravitational collapse of cold, molecular gas in the densest regions of Giant Molecular Clouds (GMCs). This correspondence between star formation and dense gas has been well established observationally on scales large and small. Across entire galaxies, both quantities have time and time again been shown to correlate exquisitely, following the empirical star formation rate-molecular gas (“Schmidt-Kennicutt”) relation. In the nearest star-forming regions in the Milky Way, the youngest protostars are preferentially found alongside the coldest, densest substructures in GMCs, which show a rich forest of molecular spectral lines. However, as social science and lawyers teach us, correlation does not necessarily imply causation. In this intriguing study, Mark Krumholz challenges the paradigm, demonstrating through simple physical arguments that stars might actually also be able to form in atomic gas under certain conditions.
But, you say, gas has to get really cold for gravity to be able to take over and cause it to collapse, and you only see this cold gas (primarily molecular hydrogen, H2) in molecular clouds, where high densities and low temperatures allow fragile molecules that would otherwise be ripped apart by harsh interstellar radiation to survive. How can diffuse H I (atomic hydrogen), which reaches densities of only up to 10 cm-3 and is seen way outside the regions in galaxies where active star formation happens, ever make stars? The answer, Krumholz shows, lies in the hierarchy of timescales* in the interstellar medium (ISM): (1) the thermal (i.e. cooling) timescale, (2) the chemical (i.e. atomic to molecular) timescale, and (3) the free-fall (i.e. gravitational) time. The latter is the time it takes for gravitationally unstable gas to fully collapse — roughly the time it takes a star to form.
The power of time
Each timescale depends on a number of physical processes, as shown in Equations (1); the variables are explained in the caption. While the expressions appear fairly complicated, many of the factors cancel when intercomparing them, so stick with me! I will now highlight here the most important dependencies for each of the three timescales.
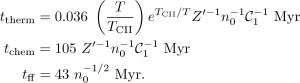
Equations (1): Thermal, chemical, and free-fall timescales. T is the initial gas temperature, TCII is the C II line temperature (~91 K), Z' is metallicity relative to solar, n0 is number density, and C1 is the "clumping factor" (which is roughly equal to 1). Note that the first two timescales depend on Z' while the free-fall time does not.
The thermal timescale is set primarily by the cooling rate, which for atomic gas happens mostly through radiation from ionized carbon (C II). This will of course depend on the abundance of carbon (i.e. metallicity): if each C II molecule radiates a certain amount, then more molecules means faster cooling. The chemical timescale is set by the rate of conversion of atomic hydrogen (H I) to molecular hydrogen (H2). This reaction takes place on the surfaces of dust grains found in the ISM, and since the formation of dust requires the presence of heavy elements, the chemical timescale also depends on metallicity. Finally, the free-fall time depends only on the gas density n0, and – crucially – not on metallicity.
Now, the shorter the timescale, the faster a process happens, and so the inverse dependence on metallicity in the thermal and chemical timescales means that as the abundance decreases, both cooling and H I-to-H2 conversion take place more slowly. On the other hand, as stated above, the free-fall time is completely unaffected by changes in metallicity. Let’s have a look at the ratio of each of the thermal and chemical timescales to the free-fall time (see Equations (2)). Here we are only showing the dependence on metallicity and have assumed characteristic ISM values for the rest of the variables**. If a ratio becomes much larger than one, that means that the process in the numerator (cooling or chemistry) takes longer than a free-fall time — i.e., stars may be able to form before the relevant process has fully taken place since the free-fall time is a proxy for star formation. From these expressions it is clear that at some fraction of solar metallicity, the chemical timescale will exceed the free-fall time while the thermal timescale is still smaller than the free-fall time. This implies that below that metallicity, the gas will form stars before having fully converted from H I to H2.
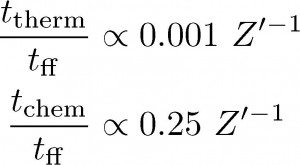
Equations (2): Timescale ratios. These were obtained from Equations (1), assuming an initial temperature of 1000 K and density of 100 cm-3. When a ratio becomes much larger than one, star formation can happen before thermal or chemical equilibrium is reached.
Implications
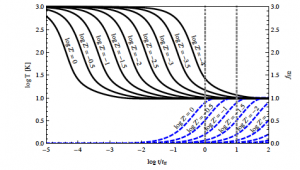
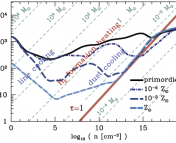
Figure 1: Time evolution of temperature (black solid lines) and molecular gas fraction (blue dotted lines) as a function of free-fall time. The various curves represent gas of different metallicity Z
After presenting these simple timescale arguments, Krumholz proceeds to study in much more detail the full balance of thermal and chemical processes that take place in (initially) atomic gas. The conclusions of this more complete analysis verify the results above. He then produces semi-analytic models exploring the time evolution of temperature and H2 fraction fH2*** in gas which is initially fully atomic and then proceeds to cool. In these models, the starts the gas at T=1000 K and fH2=0, and examines the results spanning the parameter space of density (from 1 to 103 cm-3) and metallicity (from 10-4 to 1 times solar). The results are shown in Figure 1, which reinforce the qualitative timescale argument: even at Z’=10-4 (0.01% of solar metallicity) the gas reaches around 10 K by a few free-fall times, cooling effectively. But below Z’=10-1.5 (about 3% of solar metallicity), fH2 is still less than 50% even after ten free-fall times, implying again that stars form before the gas becomes entirely molecular.
Implications and Observational Signatures
Krumholz goes on to discuss two potentially observable consequences of the above conclusions. First, if stars can form in primarily atomic gas in low metallicity systems, this means that chemical equilibrium has not yet been reached in that gas (see the first footnote below), and so observed H2 fractions should be lower than what would be predicted from equilibrium models (i.e. models that calculate fractions based on the assumption of chemical equilibrium). Second, the time measured for a galaxy to use up all its molecular gas, called the “depletion time” and defined as the H2 mass divided by the star formation rate, should be lower in these low metallicity systems. These predictions are difficult to test because CO ceases to directly correlate with H2 at metallicities below a few tenths of solar (for an observational example of this, see this astrobite by Nathan Goldbaum). Other tracers, such as extinction, dust, or C II emission will need to be used to measure H2, and compared with H I maps to derive molecular fractions. Dwarf galaxies present one possible environment in which these implications may be relevant.
There are major implications for galaxy simulations as well: since the largest physical scales needed (tens of kpc) are much bigger than the scales on which star formation takes place (fractions of a pc), the resolution in these simulations is insufficient to directly model the star formation process. Thus they often prescribe star formation to take place solely in molecular gas, and utilize equilibrium models. The results of this study suggest that both of these assumptions could potentially lead to misleading results in low metallicity systems.
Although the predictions of this paper are only relevant for a subset of the environments in which star formation takes place, the idea that stars could possibly form without molecules is nonetheless a revolutionary one. While the correlation between molecular gas and star formation does remain intact in “normal” metallicity systems, astronomers may have to get used to the idea that the relation is not as causal as has often been assumed.
*Technically, a timescale is the amount of time necessary for equilibrium to be reached; for example, in a gas in thermal equilibrium, the amount of cooling exactly balances the amount of heating. Consequently, before this time is reached, the processes are thus tacitly not in equilibrium.
**Note that the ratio of the thermal to free-fall time includes a dependence on the initial gas temperature, as can be seen in Equations (1). The numerical factors assume that the gas started at about 1000 K; the ratio changes by only a factor of a few as this starting temperature is lowered down near the C II line temperature of 91 K.
***fH2 is defined as 2 NH2/NH, so a value of 0 means fully atomic gas, while a value of 1 means entirely molecular gas.


Trackbacks/Pingbacks